Область определения функции:

Область определения функции - при каком условие существует данное выражение. Подкоренное выражение существует, когда подкоренное выражение боле или равно нулю (т.к. корень из отрицательного числа не извлекается по определению). Запишем условие:

$4x^2 -1 \geq 0$

Cогласно алгоритму решения квадратных неравенств, в рабочей зоне приравниваем к нули выражение $4x^2 -1$

$4x^{2} - 1 = 0$

$4x^{2} = 1 | : 4$

$x^{2} = \frac{1}{4}$

$x_{1}= \frac{1}{2}=0,5$

$x_{2}=-\frac{1}{2}=-0,5$

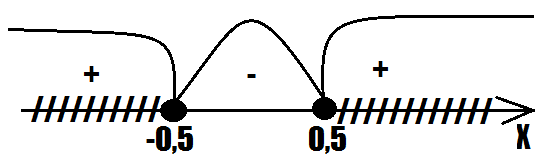
Согласно условию "больше или равно нулю" на чертеже точки будут закрашенными. При подстановке нуля в промежуток между -0,5 и 0,5 получаем знак минус, т.к. 4*0 - 1 = -1. Так как условие "больше или равно нулю", то нам нужно всё то, что стоит под знаком плюс, соответственно по чертежу получаем решение:

$x\leq-0,5$

$x\geq 0,5$

Ответ: область определения функции: x ≤ -0,5; x ≥0,5