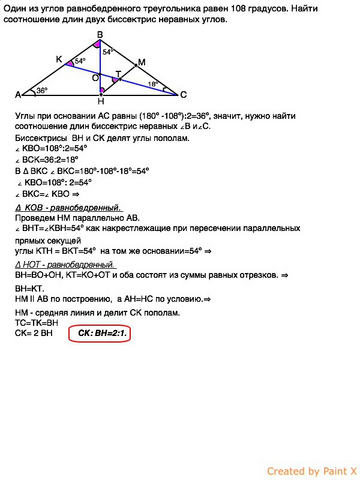
Один из углов равнобедренного треугольника равен 108 градусов. Найти соотношение длин двух биссектрис неравных углов.
Сделаем рисунок.
Пусть данный треугольник АВС, АВ=ВС
Углы при основании АС равны (180º -108º):2=36º, значит, нужно найти соотношение длин биссектрис ∠В и∠С, т.к. они не равны.
Биссектрисы ВН и СК делят углы пополам.
∠ КВО=108º:2=54º
∠ ВСК=36:2=18º
В ∆ ВКС ∠ ВКС=180º-108º-18º=54º
∠ КВО=108º:2=54º
∠ ВКС=∠ КВО ⇒
∆ КОВ - равнобедренный.
Проведем НМ параллельно АВ.
∠ ВНТ=∠КВН=54º как накрестлежащие при пересечении параллельных прямых секущей
углы КТН = ВКТ=54º на том же основании ⇒
∆ НОТ - равнобедренный.
ВН=ВО+ОН, КТ=КО+ОТ и оба состоят из суммы равных отрезков. ⇒
ВН=КТ.
НМ || АВ по построению, а АН=НС по условию.⇒
НМ - средняя линия и делит СК пополам.
ТС=ТК=ВН
СК= 2 ВН
СК:ВН=2:1.