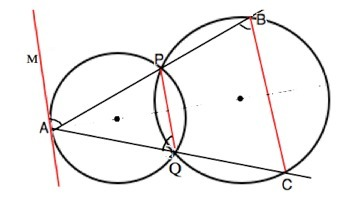
Через т.А проведем касательную АМ
АР- хорда, ∠МАР =дуга АР:2 ( свойство угла между касательной и хордой)
Вписанный ∠АQP=дуга АР:2 ( свойство вписанного угла)⇒
∠МАР=∠АQP.
∠РQC +∠PQA=180°
Во второй окружности сумма противоположных углов вписанного четырехугольника PBCQ равна 180°(свойство), ⇒
∠РQC+=180° Следовательно, ∠АВС=∠PQA.
Так как ∠PQA=∠PAM, то ∠ABC=∠BAM. Они накрестлежащие, а равенство накрестлежащих углов при пересечении двух прямых секущей – признак параллельных прямых.⇒
МА║ВС , что и требовалось доказать.