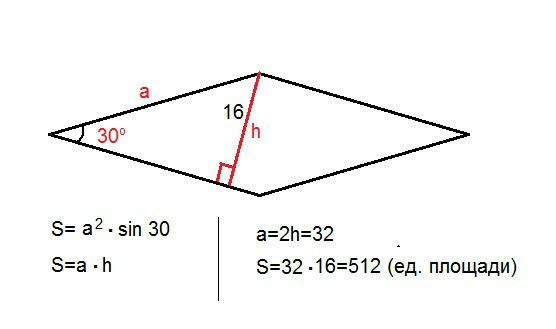
Ромб - параллелограмм.
Площадь параллелограмма можно найти по разным формулам. В данном случае можно применить:
1) S=a•h
2) S=a•a•sin α, где а- сторона ромба, h- его высота, α - угол между сторонами.
В обоих случаях нужно найти сторону.
Т.к. высота отсекает от ромба прямоугольный треугольник, в котором она - катет, противолежащий углу 30º, то сторона ромба, как гипотенуза этого треугольника, вдвое больше высоты.
а=16•2=32
S=32•16=512 (ед. площади)
или
S=32²•0,5=512 (ед. площади)