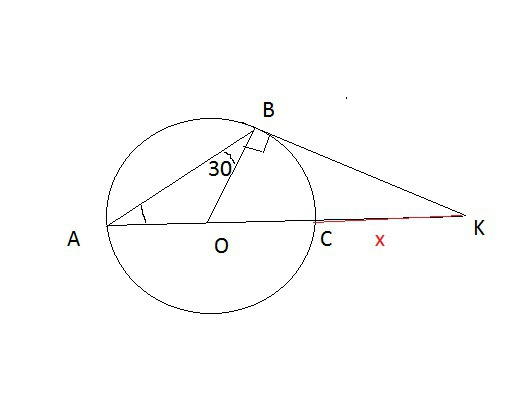
∠АВО=∠АВК-∠ОВК=120°-90°=30°
Треугольник АВО - равнобедренный (АО=ВО=3см)
∠АОВ=120° (180°-30°-30°)
По теореме косинусов
АВ²=3²+3²-2·3·3·сos120°=27
AB=3√3 см
Обозначим
СО=х
По свойству касательной и секущей:
произведение секущей на её внешнюю часть равно квадрату касательной, получаем равенство
ВК²=КС·КА
ВК²=х·(х+6)
По теореме косинусов из треугольника АВК:
АК²=АВ²+ВК²-2АВ·ВК·cos∠ABK;
(x+6)²=(3√3)²+x(x+6)-2·3√3·√x(x+6)·(-1/2);
x²+12x+36=27+x²+6x+3√3·√x(x+6);
9+6x=3√3·√x(x+6);
Возводим в квадрат
81+108х+36х²=27х²+162х
9х²-54х+81=0
х²-6х+9=0
х=3
ВК²=х(х+6)=3·(3+6)=27
ВК=3√3 см
S=AB·BK·sin∠ABK/2=(3√3)·(3√3)·√3/4=27√3/4 кв. см