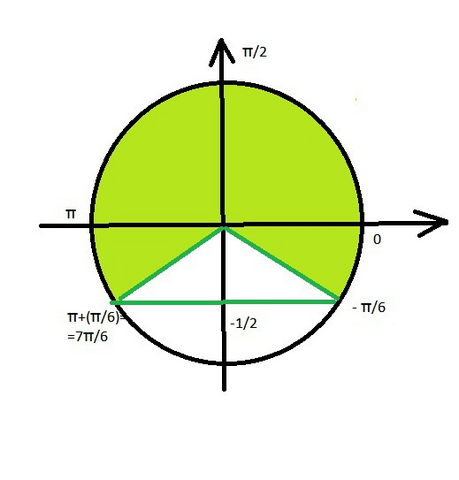
sin(x - (π/6)) ≥ -1/2.
Пусть
х - (π/6)=t, тогда
неравенство
sin t ≥ -1/2 верно при
-(π/6)+2πk ≤ t ≤ (7π/6)+2πk, k∈ Z ( cм. рисунок).
Обратная замена
-(π/6)+2πk ≤ x-(π/6) ≤ (7π/6)+2πk, k∈ Z;
прибавим (π/6) ко всем частям неравенства:
2πk ≤ x ≤ (4π/3)+2πk, k∈Z
О т в е т. (2πk; (4π/3) +2πk), k∈ Z