Объем пирамиды есть деленное на 3 произведение площади основания пирамиды на высоту.
V = (S*h)/3
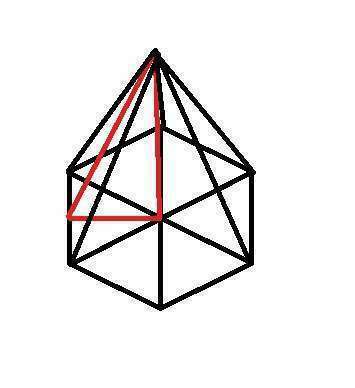
Высота дана по условию, значит, надо найти площадь основания. Зная апофему и высоту, находим высоту треугольного сегмента основания.
Делается это по т. Пифагора: корень из (15^2 - 12^2).
Корень из (15^2 - 12^2) = корень из 81 = 9.
Так как пирамида правильная, то в основании лежит правильный шестиугольник, а значит, все треугольные сегменты в основании - правильные треугольники. Зная это, по все той же теореме Пифагора найдем сторону основания.
a^2 - (a/2)^2 = 9^2
3*a^2 = 4 * 81
a^2 = (4 * 81)/3
a = корень(108) = 6 * корень(3).
Площадь основания есть не что иное, как площадь всех шести треугольных сегментов. Найдем площадь каждого из них.
Sсегмента = 0.5 * 6 * корень(3) * 9 = 27 * корень(3) см^2
Тогда площадь основания
S = 6 * Sсегмента = 6 * 27 * корень(3) = 162 * корень(3) см^2
Осталось найти искомый объем.
V = (12 *162 * корень(3))/3 = 648 * корень(3) см^3
Ответ: 648* корень(3) см^3
На рисунке в приложении показаны треугольные сегменты основания, а красным выделен треугольник: высота пирамиды - апофема боковой стороны - высота сегмента в основании.