Cosx=t
t²-(3+2p)t+6p=0
D=(3-2p)²
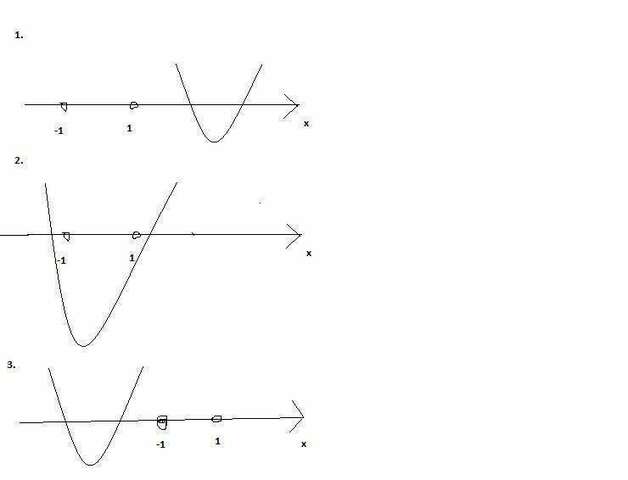
Это уравнение всегда имеет корни, да. Но в основном уравнении у нас не t, а cosx. cosx принимает значения от -1 до 1. Значит для того чтобы основное уравнение не имело корней, нужно чтобы все корни уравнения с t лежали вне промежутка [-1; 1]. Иными словами чтобы парабола задаваемая этим уравнением располагалась так как показано на прекрасных рисунках, которые я приложил.
1ый. случай задается системой
{f(-1)>0
{f(1)>0
{x0>1
2ой:
{f(-1)<0 </span>
{f(1)<0 </span>
3ий:
{f(-1)>0
{f(1)>0
{x0<-1 <br>Решаем эти системы и получаем p∈(-oo;-1/2) U (1/2;+oo).