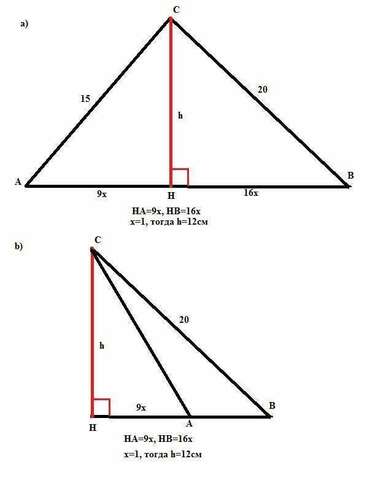
Проекция наклонной, проведенной из некоторой точки к прямой - это отрезок, соединяющий основание наклонной и основание перпендикуляра к прямой, опущенного из этой же точки.
Поскольку наклонные проведены из одной точки, то и перпендикуляр из этой же точки - это расстояние от точки до прямой.
Может быть два варианта проведения наклонных:
а) наклонные проведены по разные стороны от перпендикуляра и b) наклонные проведены по одну сторону от перпендикуляра.
Решение и ответ в обоих случаях одинаковые.
Имеем два прямоугольных треугольника с гипотенузами (наклонными) 15см и 20см и катетами (проекциями соответствующих наклонных).
Эти катеты равны 9х и 16х. Второй катет у этих треугольников общий - это перпендикуляр проведенный из данной точки к основанию. Тогда из двух прямоугольных треугольников с общим катетом - высотой нашего треугольника "h" по Пифагору имеем: : h²=15²-(9x)² (1) и h²=20²-(16x)² (2). Приравнивая (1) и (2) имеем:
225-81х²=400-256х², отсюда 175х²=175 и х=1.
Значит отрезки основания исходного треугольника равны 9см и 16см.
Тогда из любого уравнения находим искомое расстояние:
h=√(225-81)=√144=12.
Ответ: искомое расстояние равно 12см.