ОДЗ: sinx≠0
x≠πk, k∈Z
(1/sin²x)+(cosx/sinx)-3<0;<br>(1+cosxsinx-3sin²x)/sin²x<0<br>Так как sin²x ≥0 при любом х, то при х≠πk, k∈Z
1+cosxsinx-3sin²x<0<br>Заменим
1=sin²x+cos²x
sin²x+cos²x+cosxsinx-3sin²x <0<br>или
cos²x+cosxsinx-2sin²x <0<br>Делим на sin²x≠0:
сtg²x+ctgx-2<0<br>Замена переменной:
ctg x=t
t²+ t -2 <0<br>D=1+8=9
t=(-1-3)/2=-2 или t=(-1+3)/2=1
___+___(-2)___-___(1)_____+___
-2 < t <1 <br>
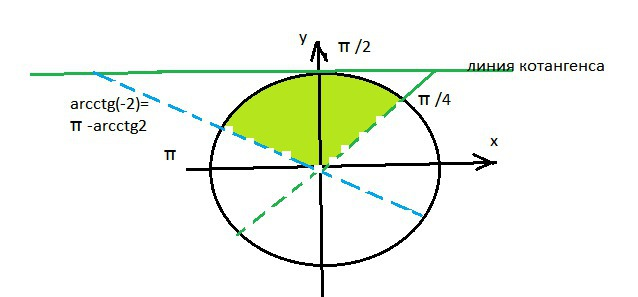
-2 ctgx <1.<br>
Cм. рисунок в приложении.
arcctg (-2)=π-arcctg2.
π-(arctg2)+πn < x< (π/4)+πn, n∈Z
О т в е т. π-(arctg2)+πn < x < (π/4)+πn, n∈Z.