Параллельно стороне треугольника, равной 5, проведена прямая. Длина отрезка этой прямой,...

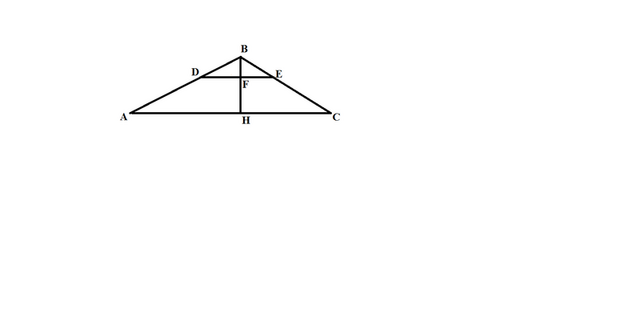
Исходя из рисунка во вложении получаем что треугольник АВС будет подобен трегольнику DBE(подобие по трем углам):

1-угол В является общим для обоих треугольников

2-угол BDE= углу ВАС как внешние односторонние ввиду параллельности DE и AC

3-угол BED= углу BCA как внешние односторонние ввиду параллельности DE и AC

Получаем, что треугольник АВС подобен трегольнику DBE. Тогда получаем коэффициент подобия:

$k=\frac{DE}{AC}=\frac{BA}{BD}=\frac{BE}{EC}=\frac{2}{5}$

Если коэффициент подобия сторон равен k, тогда коэффициент подобия площадей будет равен $k^2$ получаем:

$\frac{S_{ABC}}{S_{DBE}}=k^2=(\frac25)^2=\frac{4}{25}$

Тогда получаем:

$\frac{S_{ABC}}{S_{ADEC}}=1-\frac{S_{ABC}}{S_{DBE}}=1-\frac{4}{25}=\frac{21}{25}$

Ответ: $\frac{21}{25}$