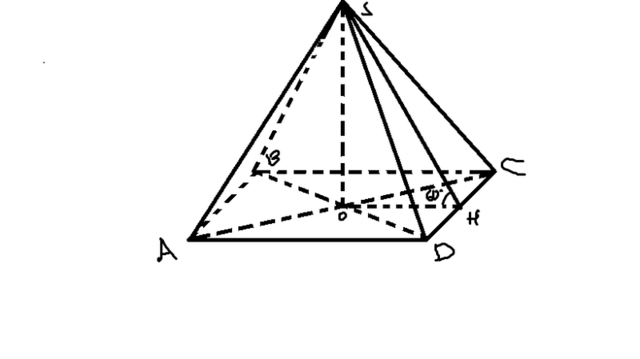
V=1/3*Sосн*H, где H - высота пирамида, Sосн. - площадь основания пирамиды.
Т.к. пирамида правильная, то в основании лежит квадрат.
Sкв.=Sосн.=10^2=100
Проведём апофему SH, тогда OH перпендиклярно DC (по обратной ТТП)
Значит угол SHO - угол между боковой гранью и основанием
уголSHO=60
Рассмотрим треугольник SHO.
OH=1/2*AD=1/2*10=5
Найдём через тангенс SO(высоту пирамиды)

Теперь найдём объём пирамиды.