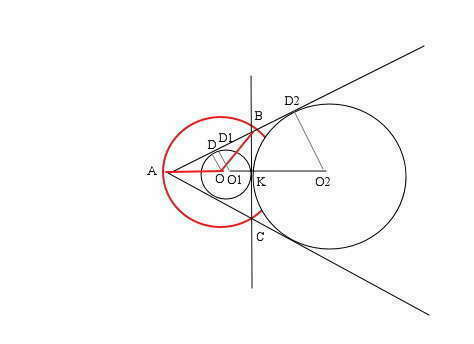
т.к. АВ касательная к обеим данным окружностям, то радиусы, проведенные в точки касания, _|_ к касательной => получившаяся фигура O1D1D2O2 ---прямоугольная трапеция...
построим из О1 высоту этой трапеции (О1Н): О1Н _|_ D2O2, О1Н || АВ
треугольники ADO и O1HO2 подобны (они прямоугольные и углы DAO и HO1O2 равны!!!)
=> AD / O1H = AO / O1O2
AO ---искомый радиус, О1О2 = 3r (r ---радиус меньшей известной окружности)
AD = AB/2 (АОВ равнобедренный, т.к. вершины треугольника лежат на описанной окружности, ОD и высота и медиана... или иначе: центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника...)
по т.Пифагора О1Н^2 = (O1O2)^2 - (HO2)^2 = (3r)^2 - r^2 = 8r^2
O1H = r*V8 = 2r*V2
AO = AD * O1O2 / O1H
AO = (V3 / 2) * 3r / (2r*V2) = 3V3 / (4V2) = 3V6 / 8