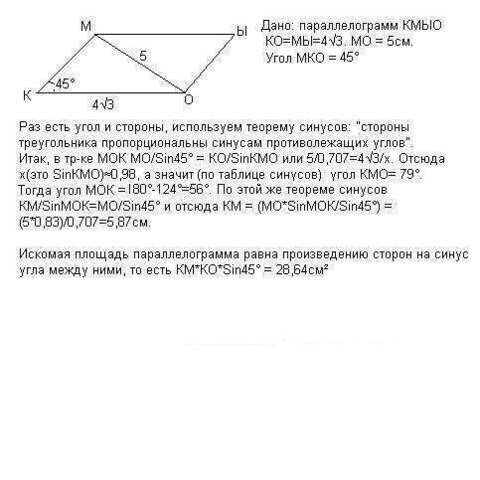
Раз есть угол и стороны, используем теорему синусов: "стороны треугольника пропорциональны синусам противолежащих углов".
Итак, в тр-ке МОК МО/Sin45° = КО/SinКМО или 5/0,707=4√3/х. Отсюда х(SinКМО)≈0,98, а значит угол КМО= 79°. Тогда угол МОК = 180°-124°=56°. По этой же теореме
КМ/SinМОК=МО/Sin45° и отсюда КМ = (МО*SinМОК/Sin45°) = (5*0,83)/0,707=5,87см.
Искомая площадь параллелограмма равна произведению сторон на синус угла между ними, то есть КМ*КО*Sin45° = 28,64см²
Проверь, пожалуйста, арифметику - у меня с ней напряг.