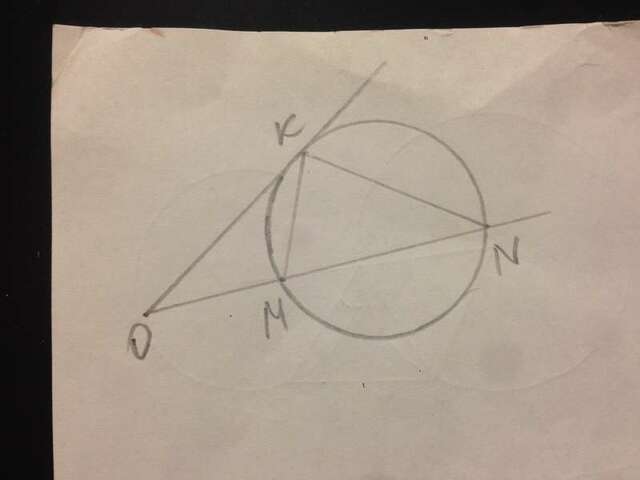
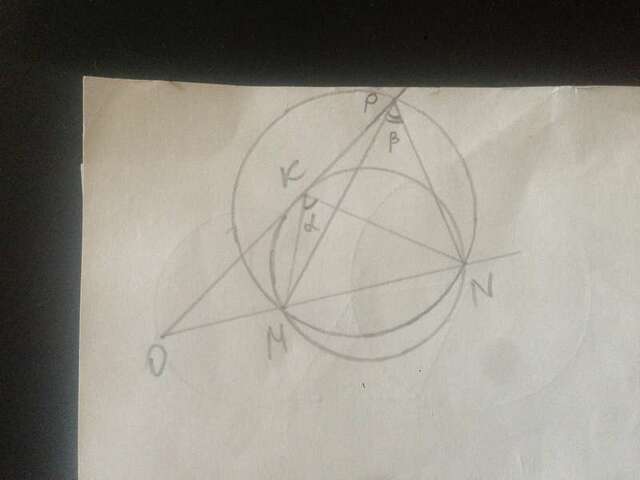Точка К, из которой будет виден отрезок МN под наибольшим углом, будет находиться на общей окружности с точками М и N. При этом OK для неё является касательной.
По свойству касательной и секущей ОК²=ОМ·ОN.
Пусть ОМ=х, тогда ОN=OM+MN=x+6,
4²=x(х+6),
х²+6х-4=0,
х1=-8, отрицательное значение не подходит,
х2=2.
ON=2+6=8 дм - это ответ.
Теперь докажем, что отрезок MN виден из точки К под большим углом.
Пусть радиус окружности около тр-ка КMN равен r.
На стороне ОК в любом месте возьмём точку Р и опишем окружность около тр-ка РMN, радиусом R. ОР для неё является секущей, а для окружности, радиусом r - касательной, значит R>r.
Формула хорды: l=2R·sin(x/2), где х - градусная мера хорды.
∠MKN=α, ∠MPN=β.
Обратим внимание, что углы α и β - это половина градусной меры хорды.
MN=2R·sinβ ⇒ sinβ=MN/2R.
MN=2r·sinα ⇒ sinα=MN/2r.
Сравним синусы, предположив, что они равны.
MN/2R=MN/2r.
1/R=1/r, но R>r, значит 1/R<1/r, значит sinβ<sinα.<br>Так как градусная мера хорды не может быть больше 180°, значит в формуле хорды 0°<α<90°, 0°<β<90°.<br>В этом диапазоне синус угла тем больше, чем больше его градусная мера,
значит α>β.
Доказано.