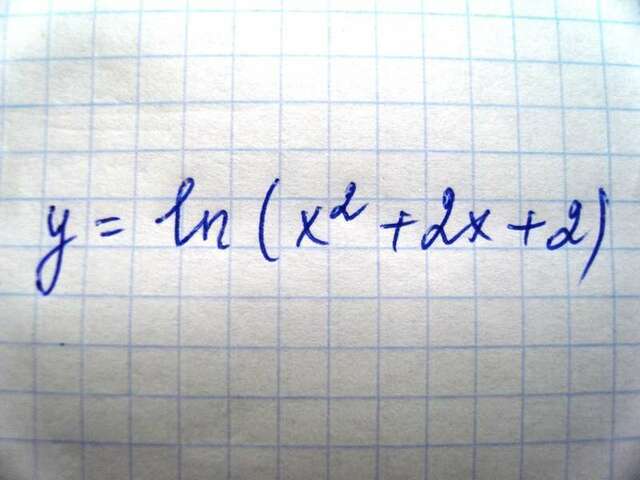Исследовать данную функцию методами дифференциального исчисления и начертить их...

Question

Исследовать данную функцию методами дифференциального исчисления и начертить их график.

Исследование и построение графика рекомендуется проводить по следующей схеме:

1. найти область существования функции;

2. исследовать функцию на непрерывность, найти точки разрыва функции и её односторонние пределы в точках разрыва;

3. выяснить, не является ли данная функция четной, нечетной;

4. найти точки экстремума функции и определить интервалы возрастания и убывания функции;

5. найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика функции;

6.найти асимптоты графика функции, если они имеются;

7. построить график функции, используя результаты исследования; при необходимости можно дополнительно находить точки графика, давая аргументы x ряд значений и вычисляя соответствующие значения y.

---

Answer 1

x^2+2x+2>0  D<0 при любых x функция определена</p>

нули функции x=0 y=ln2

ln(x^2+2x+2)=0  x^2+2x+2=1  x^2+2x+1=0 (x+1)^2=0

x=-1 у=0

y'=(2x+2)/(x^2+2x+2)

x=-1 -критическая точка, при переходе производная меняет

знак с - на +, в точке имеется минимум

функция положительна на всей области определения

x^2+2x+2<1 (x+1)^2<0, что не возможно.</p>

 

p.s. Лиза, скиньте адрес своей электронной почты, я сброшу

вам полный анализ. и график вечером только.