Точки C и D лежат ** окружности с диаметром AB. Прямые AC и BD пересекаются в точке P, а...

Question

Точки C и D лежат на окружности с диаметром AB. Прямые AC и BD пересекаются в точке P, а прямые AD и BC – в точке Q. Докажите, что прямые AB и PQ перпендикулярны.

Answer 1

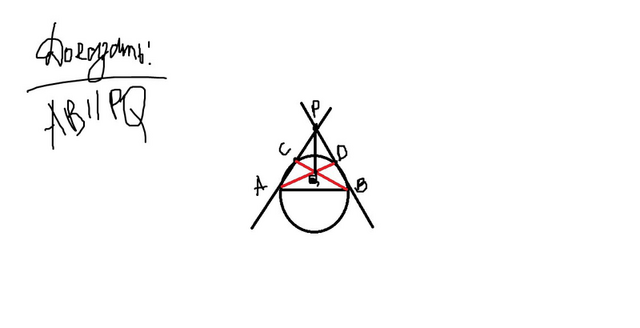
Т.к. касательная к окружности перпендикулярна к радиусу, проведённому в точку касания. Следовательно угл А= углу В=90 градусам. По правилу , что отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. Следовательно РА=РВ. Рассмотрим треугольники АДВ и ВСА они равны. И если рассмотрим треугольник АQР и BQP они тоже равны. 

---

Comments

угол а не может быть равен углу б ведь тогда сумма углов треугольника больше 180 градусов