![\sqrt{x} -9 \sqrt[4]{x} +11 \geq 0 \sqrt{x} -9 \sqrt[4]{x} +11 \geq 0](https://tex.z-dn.net/?f=+%5Csqrt%7Bx%7D+-9+%5Csqrt%5B4%5D%7Bx%7D+%2B11+%5Cgeq+0)
![( \sqrt[4]{x})^2 -9 \sqrt[4]{x} +11 \geq 0 ( \sqrt[4]{x})^2 -9 \sqrt[4]{x} +11 \geq 0](https://tex.z-dn.net/?f=%28+%5Csqrt%5B4%5D%7Bx%7D%29%5E2+-9+%5Csqrt%5B4%5D%7Bx%7D+%2B11+%5Cgeq+0)
![( \sqrt[4]{x})^2 -9 \sqrt[4]{x} +11 \geq 0 ( \sqrt[4]{x})^2 -9 \sqrt[4]{x} +11 \geq 0](https://tex.z-dn.net/?f=%28+%5Csqrt%5B4%5D%7Bx%7D%29%5E2+-9+%5Csqrt%5B4%5D%7Bx%7D+%2B11+%5Cgeq+0)
Замена
![\sqrt[4]{x} =t \geq 0 \sqrt[4]{x} =t \geq 0](https://tex.z-dn.net/?f=+%5Csqrt%5B4%5D%7Bx%7D+%3Dt+%5Cgeq+0)




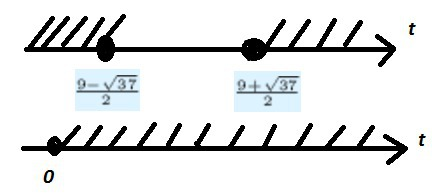
![t\in[0;\frac{9- \sqrt{37} }{2}]\cup[\frac{9+ \sqrt{37} }{2};+\infty) t\in[0;\frac{9- \sqrt{37} }{2}]\cup[\frac{9+ \sqrt{37} }{2};+\infty)](https://tex.z-dn.net/?f=t%5Cin%5B0%3B%5Cfrac%7B9-+%5Csqrt%7B37%7D+%7D%7B2%7D%5D%5Ccup%5B%5Cfrac%7B9%2B+%5Csqrt%7B37%7D+%7D%7B2%7D%3B%2B%5Cinfty%29)
т.е.
![0 \leq \sqrt[4]{x}\leq\frac{9- \sqrt{37} }{2} 0 \leq \sqrt[4]{x}\leq\frac{9- \sqrt{37} }{2}](https://tex.z-dn.net/?f=0+%5Cleq+%5Csqrt%5B4%5D%7Bx%7D%5Cleq%5Cfrac%7B9-+%5Csqrt%7B37%7D+%7D%7B2%7D)
и
![\sqrt[4]{x} \geq \frac{9+ \sqrt{37} }{2} \sqrt[4]{x} \geq \frac{9+ \sqrt{37} }{2}](https://tex.z-dn.net/?f=+%5Csqrt%5B4%5D%7Bx%7D++%5Cgeq+%5Cfrac%7B9%2B+%5Csqrt%7B37%7D+%7D%7B2%7D)
- решения этих дух неравенств и будут решением исходного неравенства
Отдельно первое:
![0 \leq \sqrt[4]{x} \leq \frac{9- \sqrt{37} }{2} 0 \leq \sqrt[4]{x} \leq \frac{9- \sqrt{37} }{2}](https://tex.z-dn.net/?f=0+%5Cleq+%5Csqrt%5B4%5D%7Bx%7D+%5Cleq++%5Cfrac%7B9-+%5Csqrt%7B37%7D+%7D%7B2%7D)
![\left \{ {{ \sqrt[4]{x} \geq 0 } \atop {\sqrt[4]{x} \leq \frac{9- \sqrt{37} }{2}}} \right. \left \{ {{ \sqrt[4]{x} \geq 0 } \atop {\sqrt[4]{x} \leq \frac{9- \sqrt{37} }{2}}} \right.](https://tex.z-dn.net/?f=+%5Cleft+%5C%7B+%7B%7B+%5Csqrt%5B4%5D%7Bx%7D+%5Cgeq+0+%7D+%5Catop+%7B%5Csqrt%5B4%5D%7Bx%7D+%5Cleq++%5Cfrac%7B9-+%5Csqrt%7B37%7D+%7D%7B2%7D%7D%7D+%5Cright.+)
решением первого неравенства системы есть:

второго:

и вместе решением системы будет:

отдельно второе:
![\sqrt[4]{x} \geq \frac{9+ \sqrt{37} }{2} \sqrt[4]{x} \geq \frac{9+ \sqrt{37} }{2}](https://tex.z-dn.net/?f=%5Csqrt%5B4%5D%7Bx%7D+%5Cgeq+%5Cfrac%7B9%2B+%5Csqrt%7B37%7D+%7D%7B2%7D)

Объединяем первое и второе:

![x\in[0;(\frac{9- \sqrt{37} }{2})^4]\cup[(\frac{9+ \sqrt{37} }{2})^4;+\infty) x\in[0;(\frac{9- \sqrt{37} }{2})^4]\cup[(\frac{9+ \sqrt{37} }{2})^4;+\infty)](https://tex.z-dn.net/?f=x%5Cin%5B0%3B%28%5Cfrac%7B9-+%5Csqrt%7B37%7D+%7D%7B2%7D%29%5E4%5D%5Ccup%5B%28%5Cfrac%7B9%2B+%5Csqrt%7B37%7D+%7D%7B2%7D%29%5E4%3B%2B%5Cinfty%29)
Ответ:
![[0;(\frac{9- \sqrt{37} }{2})^4]\cup[(\frac{9+ \sqrt{37} }{2})^4;+\infty) [0;(\frac{9- \sqrt{37} }{2})^4]\cup[(\frac{9+ \sqrt{37} }{2})^4;+\infty)](https://tex.z-dn.net/?f=%5B0%3B%28%5Cfrac%7B9-+%5Csqrt%7B37%7D+%7D%7B2%7D%29%5E4%5D%5Ccup%5B%28%5Cfrac%7B9%2B+%5Csqrt%7B37%7D+%7D%7B2%7D%29%5E4%3B%2B%5Cinfty%29)
---------------------------------------------
![\sqrt[3]{x^2+7x-8}* \sqrt{x+9} \leq 0 \sqrt[3]{x^2+7x-8}* \sqrt{x+9} \leq 0](https://tex.z-dn.net/?f=+%5Csqrt%5B3%5D%7Bx%5E2%2B7x-8%7D%2A+%5Csqrt%7Bx%2B9%7D+%5Cleq+0++)
Рассмотрим случай, когда

,
это случай, когда

В этом случае мы можем спокойно поделить неравенство на этот квадратный корень и получим:
![\sqrt[3]{x^2+7x-8} \leq 0 \sqrt[3]{x^2+7x-8} \leq 0](https://tex.z-dn.net/?f=%5Csqrt%5B3%5D%7Bx%5E2%2B7x-8%7D+%5Cleq+0)
и отложим этот случай на время
второй случай:

, т.е

в этом случае наше алгебраическое неравенство превращается в правдивое числовое неравенство

т.е.

- одно из решений исходного неравенства
вернемся к первой ветке:
![\left \{ {{ \sqrt[3]{x^2+7x-8} \leq 0 } \atop {x\ \textgreater \ -9}} \right. ;
\left \{ {{ \sqrt[3]{(x-8)(x-1)} \leq 0 } \atop {x\ \textgreater \ -9}} \right. \left \{ {{ \sqrt[3]{x^2+7x-8} \leq 0 } \atop {x\ \textgreater \ -9}} \right. ;
\left \{ {{ \sqrt[3]{(x-8)(x-1)} \leq 0 } \atop {x\ \textgreater \ -9}} \right.](https://tex.z-dn.net/?f=+%5Cleft+%5C%7B+%7B%7B+%5Csqrt%5B3%5D%7Bx%5E2%2B7x-8%7D+%5Cleq+0+%7D+%5Catop+%7Bx%5C+%5Ctextgreater+%5C+-9%7D%7D+%5Cright.+%3B%0A+%5Cleft+%5C%7B+%7B%7B+%5Csqrt%5B3%5D%7B%28x-8%29%28x-1%29%7D+%5Cleq+0+%7D+%5Catop+%7Bx%5C+%5Ctextgreater+%5C+-9%7D%7D+%5Cright.+)
видим, что при

и

первое алгебраическое неравенство превращается в верное числовое неравенство

и также оба этих значения удовлетворяю второе неравенство системы, т.е. эти два значения являются так же решениями исходного неравенства.
теперь умножаем наше неравенство на
![( \sqrt[3]{(x-8)(x-1)} )^2\ \textgreater \ 0 ( \sqrt[3]{(x-8)(x-1)} )^2\ \textgreater \ 0](https://tex.z-dn.net/?f=%28+%5Csqrt%5B3%5D%7B%28x-8%29%28x-1%29%7D+%29%5E2%5C+%5Ctextgreater+%5C+0)
убирая куб

решение неравенства:
![x\in[1;8] x\in[1;8]](https://tex.z-dn.net/?f=x%5Cin%5B1%3B8%5D)
Учитывая отброшенную начале -9:
![x\in\{-9\}\cup[1;8] x\in\{-9\}\cup[1;8]](https://tex.z-dn.net/?f=x%5Cin%5C%7B-9%5C%7D%5Ccup%5B1%3B8%5D)
Ответ:
![\{-9\}\cup[1;8] \{-9\}\cup[1;8]](https://tex.z-dn.net/?f=%5C%7B-9%5C%7D%5Ccup%5B1%3B8%5D)