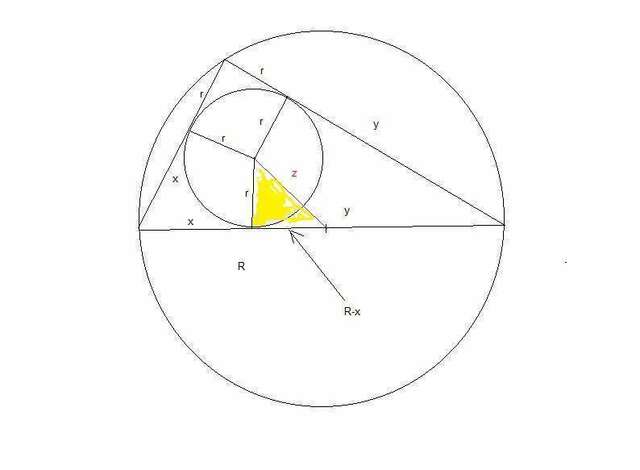
решил выкласть решение.
смотри рисунок.
понятно, что отрезки катетов есть отрезки касательных, они равны.
Сделаем все обозначения.
гипотенуза будет 1) х+у=2R
По т. Пифагора
(x+r)²+(y+r)²=(x+y)²
раскрывая, получаем
r(x+y)+r²=xy подставляем сюда 1) и получаем
xy=2Rr+r²
из 1) выделяем у и подставляем, приводим и т.д. и получаем
x²-2Rx+(2Rr+r²)=0
D=4(R²-2Rr-r²)
x=R+/- √(R²-2Rr-r²) но т.к. x≤R то тогда
x=R- √(R²-2Rr-r²)
ну а нижний катет желтого треугольника тогда равен
√(R²-2Rr-r²)
найдем гипотенузу желтого
r²+(√(R²-2Rr-r²) )²=z²
z²=R²-2Rr
z=√(R*(R-2r))
P.S. Здесь я не сделал исследование по поводу допустимых значений радиусов. Просто не захотел, т.к. удлиняет решение.