Х=-4; х=0; х=4 - точки, в которых подмодульное выражение меняет знак.
Эти точки разбивают числовую прямую на 4 промежутка.
Раскрываем знак модуля на каждом промежутке:
(-∞;-4]
|x|=-x
|x·(4+x)|=x(4+x)
Уравнение принимает вид:
х(4+х)=2
х²+4х-2=0
D=16+8=24
x₁=-2-√6
х=-2+√6∉(-∞;-4], потому не является корнем данного уравнения
(-4;0]
|x|=-x
|x·(4+x)|=-x(4+x)
Уравнение принимает вид:
-х(4+х)=2
х²+4х+2=0
D=16-8=8
x₂=-2-√2 х₃=-2+√2
оба корня принадлежат промежутку (-4;0]
(0;4]
|x|=x
|x·(4-x)|=x(4-x)
Уравнение принимает вид:
х(4-х)=2
х²-4х+2=0
D=16-8=8
x₄=2-√2 х₅=2+√2
оба корня принадлежат промежутку (0;4]
(4;+∞)
|x|=x
|x·(4-x)|=-x(4-x)
Уравнение принимает вид:
-х(4-х)=2
х²-4х-2=0
D=16+8=24
x₆=2+√6
х=2-√6 не принадлежит промежутку (4;+∞), потому не является корнем данного уравнения
О т в е т. Уравнение имеет 6 корней
x₁=-2-√6; x₂=-2-√2; х₃=-2+√2; x₄=2-√2; х₅=2+√2; x₆=2+√6.
2 способ.
Графический
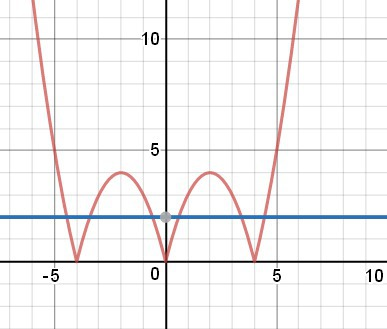
Строим графики
у=|x(4-|x|)| и у=2.
См. рис. в приложении.