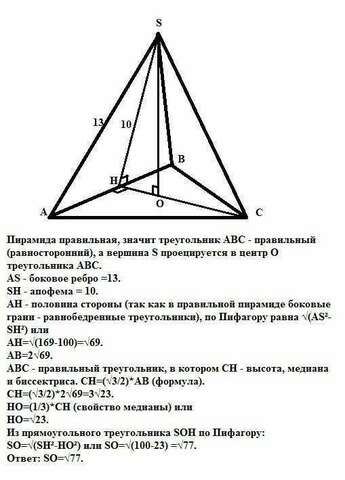
Пирамида правильная, значит треугольник АВС - правильный (равносторонний), а вершина S проецируется в центр О треугольника АВС.
AS - боковое ребро =13.
SH - апофема = 10.
АН - половина стороны (так как в правильной пирамиде боковые грани - равнобедренные треугольники), по Пифагору равна √(AS²-SH²) или
АН=√(169-100)=√69.
АВ=2√69.
АВС - правильный треугольник, в котором СН - высота, медиана и биссектриса. СН=(√3/2)*АВ (формула).
СН=(√3/2)*2√69=3√23.
НО=(1/3)*СН (свойство медианы) или
НО=√23.
Из прямоугольного треугольника SOH по Пифагору:
SO=√(SH²-HO²) или SO=√(100-23) =√77.
Ответ: SO=√77.