Противоположные стороны параллелограмма равны и параллельны. Противолежащие углы параллелограмма равны.
-----------------
Обозначим равные отрезки сторон параллелограмма одинаковыми буквами. :
По условию АЕ=СК примем=а
По условию ВF=MD примем=k
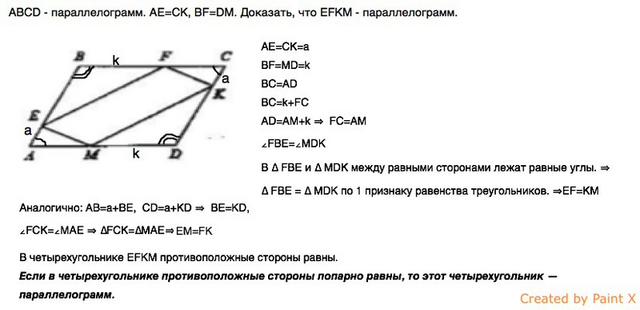
BC=AD равные стороны параллелограмма.
BC=k+FC
AD=AM+k ⇒
FC=AM
∠FBE=∠MDK
В ∆ FBE и ∆ MDK между равными сторонами лежат равные углы. ⇒
∆ FBE = ∆ MDK по 1 признаку равенства треугольников. ⇒
EF=KM
Аналогично доказывается равенство ∆ МАЕ и FCK.
AB=a+BE, CD=a+KD ⇒
BE=KD,
∠FСК=∠MАЕ ⇒ ∆FСК=∆MАЕ⇒
EM=FK
В четырехугольнике EFKМ противоположные стороны равны.
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
EFKМ— параллелограмм, ч.т.д.