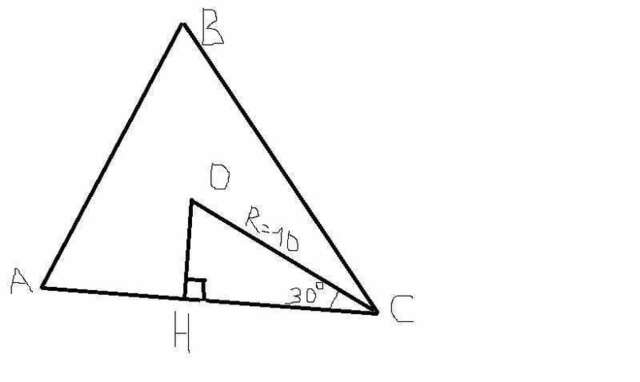
Так как О - центр описанной окружности, исходя из условий задачи, то расстояние от О долюбой вершины будет 10 см. В данном случае до А тоже 10 см. Пусть ОН - перпендикуляр, опущенный на АС. Заметим, что его длину и нужно найти. Рассмотрим треугольник ОСН. В данном случае нам известна ОC=10 см. Так как угол ОСН равен углу ОСА равен 30 градусам, то ОН равен произведению ОС на синус угла ОСН.


OH=OC*0,5
OH=10*0,5
OH=5 см
Ответ: расстояние от точки О до стороны АС равно 5.