Sin3x+sinx-sin2x=2cosx*(cosx-1)

Question

Sin3x+sinx-sin2x=2cosx*(cosx-1)

Answer 1

sin3x+sinx-sin2x=2cosx*(cosx-1)

(sin3x+sinx)-sin2x=2cosx*(cosx-1) - сумма синусов

2*sin(4x/2)*cos(2x/2) -sin2x = 2*cosx*(cosx-1)

 2*sin(2x)*cos(x) -sin2x = 2*cosx*(cosx-1)

2*(2*sinx*cosx)*cosx - 2*sinx*cosx =  2*cosx*(cosx-1)  

 

 2*sinx*cosx * (2cosx - 1) - 2cosx(cosx-1) = 0

 2cosx*(sinx* (2cosx - 1) - cosx+1)=0

 2cosx*(sin2x - cosx)=0

cosx=0 или  sin2x - cosx=0

cosx=0, x=pi/2 + pi*k

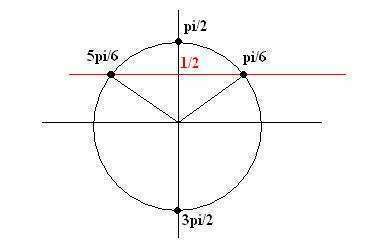
 sin2x - cosx=0, 2*sinx*cosx - cosx=0, cosx*(2sinx-1)=0, sinx=1/2, x=pi/6+2pi*k и x=5pi/6 + 2pi*k

Ответ:  x=pi/2 + pi*k,  x=pi/6+2pi*k и x=5pi/6 + 2pi*k, k - целое число.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---