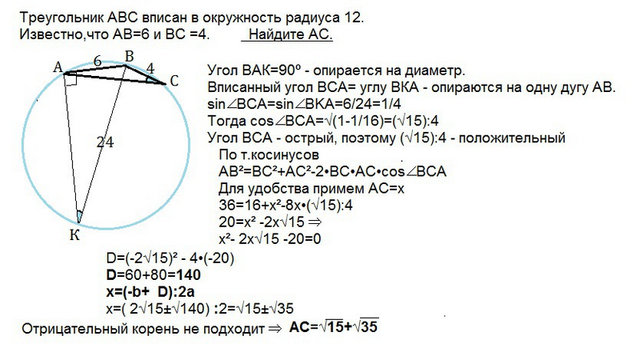
Из В проведем диаметр окружности ВК.
Угол ВАК=90º - опирается на диаметр.
Вписанный угол ВСА= углу ВКА - опираются на одну дугу AB.
sin∠ВСА=sin∠BKA=6/24=1/4
Тогда cos∠ВСА=√(1-1/16)=(√15):4
Угол ВСА - острый, поэтому (√15):4 - положительный
По т.косинусов
АВ²=ВС²+AC² - 2•BC•AC•cos∠ВСА
Для удобства примем АС=х
36=16+х²-8х•(√15):4
20=х² - 2x√15 ⇒
х²- 2x√15 -20=0
D=(-2√15)² - 4•(-20)
D=60+80=140
х=( 2√15±√140):2=√15±√35
Отрицательный корень не подходит ⇒
АС=√15+√35