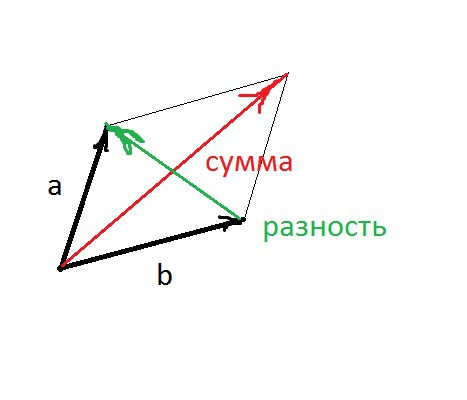
Сумма векторов a и b, имеющих общее начало, это диагональ параллелограмма, построенного на этих векторах, и исходящая из общей точки.
Разность векторов a и b, имеющих общее начало, это диагональ
параллелограмма, построенного на этих векторах и соединяющая концы векторов а и b.
Диагонали равны у прямоугольника и квадрата.
Ответ. угол 90°