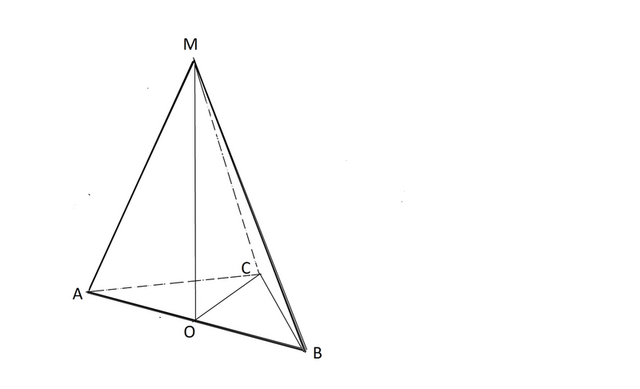
Гипотенуза АВ прямоугольного треугольника равна 10 см
Точка М находится на расстоянии 13 см от каждой его вершины.
Найдите расстояние от точки М до плоскости треугольника.
Задача больше содержит рассуждения, чем вычисления.
Треугольник АВС - прямоугольный.
Поскольку точка М находится на равном расстоянии от его вершин, проекции наклонных АМ=СМ=ВМ также равны.
Такое в прямоугольном треугольнике возможно тогда, когда к гипотенузе проведена медиана этого треугольника, так как медиана прямоугольного треугольника равна половине гипотенузы.
Расстояние от точки до плоскости измеряется длиной перпендикуляра, опущенного из точки на эту плоскость.
Следовательно, основанием перпендикуляра из М к плоскости треугольника АСВ является середина О гипотенузы АВ треугольника АСВ
⇒ АО=10:2=5, а катет МО треугольника АОМ, найденный по т.Пифагора, равен 12см.
Я не даю вычисления, они просты. К тому же, если вспомнить, что при гипотенузе 13 и одном из катетов 5 - второй катет 12, т.к. это одна из троек Пифагора ( 13, 12,5), можно и не вычислять это расстояние.
Ответ:Расстояние от точки М до плоскости треугольника равно 12 см