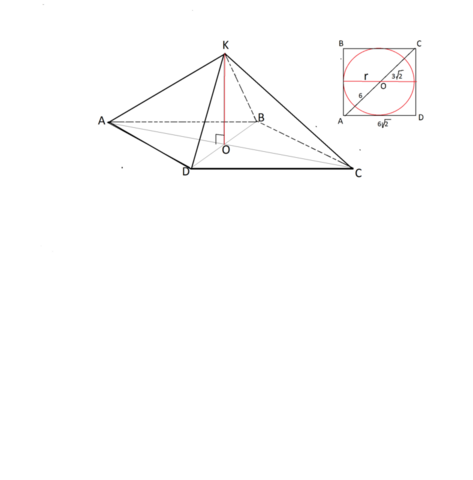
Основанием правильной четырехугольной пирамиды является квадрат.
Радиус вписанной в квадрат окружности равен половине его стороны.
Следовательно, сторона квадрата равна
2r=6√2.
Основание высоты правильной четырехугольной пирамиды находится в центре квадрата - в центре О вписанной окружности.
Высоту КО найдем из прямоугольного треугольника, образованного
ребром АК пирамиды - гипотенуза;
половина АО диагонали квадрата - катет;
высота КО -катет.
Диагональ основания D равна а√2 и
АС равна 6√2·√2=12,
ее половина АО - 6
По теореме Пифагора найдем высоту:
Н=√(АК² -АО²)=√(100-36)=8