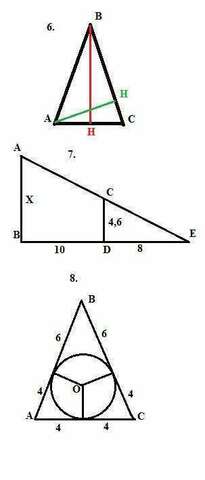
6. Боковая сторона равнобедренного треугольника АВС равна 10см, а высота составляет 6см. Найти основание АС.
Решение.
В условии не сказано, проведена ли высота к основанию треугольника (1) или к его боковой стороне (2).
1) Треугольник равнобедренный, следовательно его высота, проведенная к основанию, является и медианой. Тогда в прямоугольном треугольнике АВН, образованном боковой стороной АВ (гипотенуза), высотой ВН (катет) и половиной основания треугольника АН (второй катет) найдем по Пифагору эту половину основания. АН=√(АВ²-ВН²) или АН=√(100-36)=8см. Тогда АС=2*АН или АС=2*8=16см.
Ответ: АС=16см.
2). Если высота АН проведена к боковой стороне ВС, то из прямоугольного треугольника АВН по Пифагору находим отрезок ВН=√(100-36)=8см. Тогда отрезок НС=10-8=2см. Из прямоугольного треугольника АНС по Пифагору найдем АС.
АС=√(АН²+НС²) или АС=√(36+4)=2√10см.
Ответ: АС=2√10см.
7. Фонарь освещает дерево высотой 4,6м, находящееся на расстоянии 10м от
него. Длина тени, отбрасываемой деревом, равна 8м. Найти высоту, на
которой находится фонарь.
Решение.
Пусть высота фонаря АВ=Х, высота дерева СD=4,6м, расстояние от фонаря до дерева ВD=10м, длина тени DE=8м. Тогда треугольники EDC и ЕВА подобны, так как CD параллельна АВ (и дерево и фонарь перпендикулярны земле). Из подобия имеем:
ВЕ/DE=Х/CD. Отсюда Х=ВЕ*CD/DE или Х=18*4,6/8=10,35м.
Ответ: высота фонаря равна 10,45м.
8. В равнобедренный треугольник вписана окружность. Точки касания этой окружности с боковыми сторонами делят их на отрезки 4см и 6см, считая от основания. Найти периметр треугольника.
Решение.
Отрезки сторон от вершин треугольника до точек касания с вписанной окружностью являются касательными к этой окружности, проведенными из одной точки и по свойству касательных из одной точки равны. таким образом, основание треугольника АС равно 4см+4см=8см. Так как боковые стороны треугольника равны 4см+6см=10см, периметр треугольника равен Р=10+10+8=28см.
Ответ: периметр Рabc=28см.