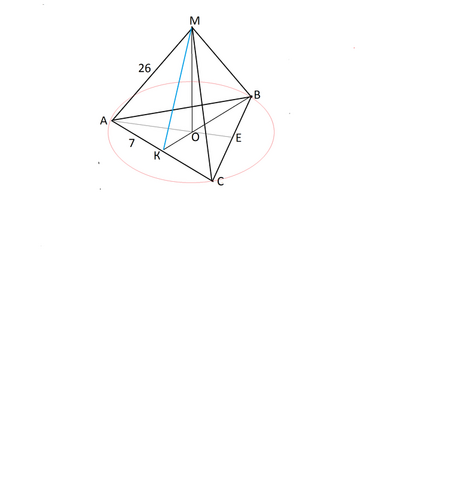
Дана правильная треугольная пирамида
со стороной основания 14 и боковым ребром 26.
Найти:
площадь боковой поверхности
площадь полной поверхности
объем.
---------------------
Площадь боковой поверхности пирамиды состоит из площади трех граней - равнобедренных треугольников с основанием 14 и боковыми сторонами 26.
Sтр-ка=аh:2
Высоту h такого треугольника найдем по т. Пифагора из его половиы -
прямоуголього треугольника АМК.
МК=√(АМ²-АК²)
МК=√(26²-7²)=√(676-49)=√627
S грани=МК·АС:2=7√627 ≈175.27977 ≈175,28
Sбок=3·7√627 =21√627
или ≈525,84
Полная поверхость пирамиды - сумма площади боковой поверхности и площади основания.
Площадь основания найдем по формуле:
Sосн=(a²√3):4
Sосн=(14²√3):4=196√3):4=49√3 ≈84,87
Sполн= 21√627+49√3=7√3(3√209+7)
или ≈ 525,84+84,87= ≈610,71
Объем пирамиды равен одной трети произведения площади основания на высоту.
Высоту трапеции следует найти.
Для этого рассмотрим треугольник АОМ.
АО- отрезок высоты, равный радиусу окружности, описанной вокруг правильного треугольника АВС, и равен он 2/3 высоты АЕ треугольника АВС.
АЕ по формуле высоты правильного треугольника
АЕ=(а√3):2=14√3):2=7√3
МО=√АМ²-АО²)
МО=√{(26²-(7√3)²}=√ 529=23
V=(23·49√3):3= 1127√3):3
или ≈650,67
-----------------
Нельзя сказать. что результат вычислений привычен, но из этих величин получается именно так.
Проверено несколько раз