Постройте график кусочно-заданной функции y=f(x), которая ** каждом промежутке вида...

Question

Постройте график кусочно-заданной функции y=f(x), которая на каждом промежутке вида (m;m+1) где m-произвольно целое число, определена равенством: f(x)=2m.
Найдите все значения k, при которых прямая y=kx пересекает график y=f(x) не менее, чем в девяти точках. Заранее Спасибо!!!

Comments

при 10 точках пересечения k принадлежит (1.8;2.25)

---

а тут получается что при k>=2

---

во всех точках (m;2m)

---

Нет, одновременно и выше и ниже она пересекает только при k=2.

---

я имею ввиду, одновременно

---

для 10 точек. да. Я же выше расписал, при каких k она будет выше пересекать, а при каких ниже

---

18/10<k<18/8 а при этом значении прямая будет пересекать и ниже и выше оси ox?

---

для всех 2<k<18/8 она будет пересекать только точки ниже оси иксов и на ней. При всех 18/10<k<2 она пересекает точки выше оси иксов и на ней.

---

При не менее 10 точках у вас прямая должна проходить левее точки (10;18) и правее точки (-8;-18). соответственно 18/10<k<18/8

---

это же не может быть

Answer 1

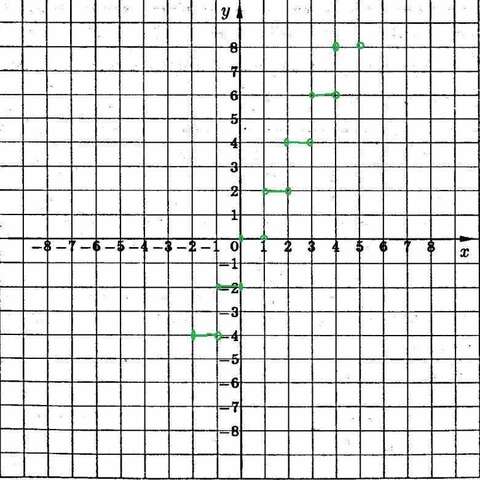
На (1;2)   f(x)=2
на (2;3)   f(x)=4
на (3;4)   f(x)=6
на (4;5)   f(x)=8
на (5;6)   f(x)=10
и т. д.
график см. рисунок в приложении.
Обратите внимание, ни крайне левой точки, ни крайне правой точки на ступеньках нет
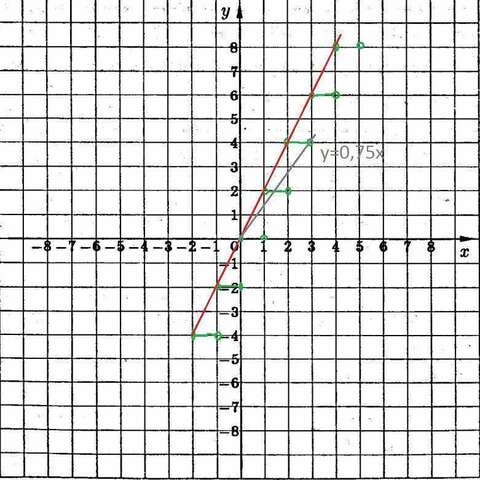
Если соединить начало координат и левые края ступенек в верхней полуплоскости, получим прямую у=2х.
Но k=2 не является ответом, так как левые края ступенек не являются точками графика, как и правые.
у=2х  и у=0,75 х не удовлетворяют условию. См. рисунок 2.
Сужаем угол.

Рассмотрим прямую, проходящую через точку (0;0) и точку (11;
20)
Эта прямая будет пересекать график в 9 точках
на отрезке, где
f(x)=2
f(x)=4
f(x)=6
f(x)=8
f(x)=10
f(x)=12
f(x)=14
f(x)=16
f(x)=18

В условии был интервал (m;m+1). Потом стал [m;m+1).
Значит к=2 входит в ответ.
Прямая у=0,75х (проходит через (0;0) и (3;4) будет иметь одну точку пересечения.
Прямая у=1,8х (проходящая через точки (0:0)и (9;18) девять.
 При 1,8 В нижней 2 Ответ (1,8;2,25)

---

---

Comments

В нижней 2<=k<18/8=2,25. Прямая, проходящая через правый край ступеньки f(x)=-18, т.е точку (-8;-18)

---

все понятно

---

для 10

---

Вам для 10 точек или 9? Не надо разделять., весь интервал включая k=2 удовлетворяет условию.

---

так получается, что в ответ надо писать два значения k 2<k<18/8 и 18/10<k<2?

---

вернее k между 16/9 и 16/7 для 9 точек

---

Нет, не 18/8, а 16/8. Надо не забывать, что (0,0) всегда точка пересечения.

---

Ответ (1,8;2,25)

---

В условии был интервал (m;m+1). Потом стал [m;m+1). Значит к=2 входит в ответ. Прямая у=0,75х будет иметь одну точку пересечения. Прямая у=1,8х девять При 1,8<k<=2 ,будет более девяти. Это в верхней полуплоскости.

---

да, для 10 от 18/10 до 18/8