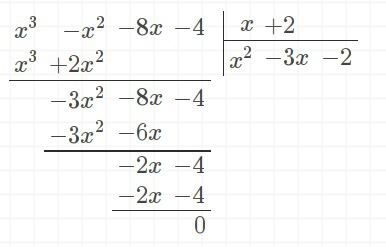Прежде всего нужно попробовать подставить предельную точку в выражение.
Возможно, предел вычисляется и без преобразований. Подставляем -2 в
числитель и знаменатель и получаем неопределённость (0/0). Это значит,
что -2 является корнем как верхнего, так и нижнего уравнения. Числитель
раскладывается в виде суммы кубов, а знаменатель нужно делить на (x+2)
столбиком. После этого сокращаем (x+2) в числителе и знаменателе и
проверяем, избавились ли мы от неопределённости. Радуемся:)

Прикрепил деление многочленов на скриншоте.