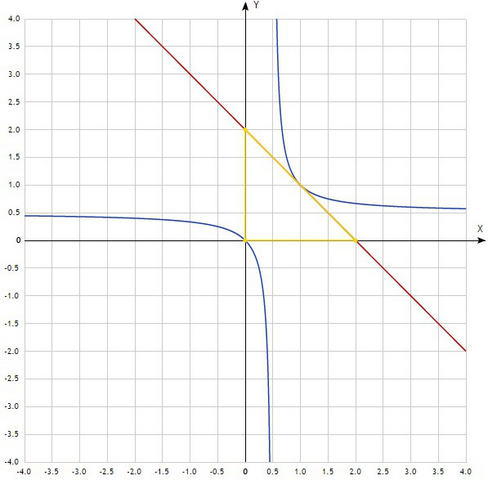
Составим уравнение касательной
y=f(x₀)+f'(x₀)(x-x₀)
Для этого найдём значение функции в точке х₀
f(1)=(2*1)/(4*1-2)=2/2=1,
и значение производной в этой точке
f'(x₀)=((2x)/(4x-2))'=((2x)'*(4x-2)-(2x)*(4x-2)')/(4x-2)²=(2*(4x-2)-(2x)*4)/(4x-2)²=
=-4/(4x-2)²
f'(1)=-4/(4*1-2)²=-4/4=-1
Уравнение касательной будет выглядеть так:
y=1+(-1)*(x-1)=1-x+1=2-x
Получаем что при х=0 у=2, а при у=0 х=2. Значит треугольник равносторонний с боковыми сторонами равными 2 ед. и прямоугольный, так как ограничен осями координат. По формуле площади прямоугольного треугольника находим площадь:
S=(1/2)*2*2=2 ед².