Y = x^(x/4) / x^2 = x^(x/4 - 2)
1) Область определения: x > 0
2) Пересечений с осями нет, x =/= 0; y =/= 0
3) Функция не четная и не нечетная, непериодическая
4) Точка разрыва и Вертикальная асимптота: x = 0.
Неустранимый разрыв 2 рода.
5) Критические точки
y ' = x^(x/4 - 2)*ln(x/4 - 2)*1/4 + (x/4 - 2)*x^(x/4 - 3) = 0
По области определения логарифма x/4 - 2 > 0; x > 8
x^(x/4 - 3)*(ln(x/4 - 2)*x/4 + x/4 - 2) = 0
x^(x/4 - 3) > 0 при любом x > 0, поэтому
ln((x-8)/4)*x/4 + (x-8)/4 = 1/4*(x*ln((x-8)/4) + x-8) = 0
x*ln((x-8)/4) + x - 8 = 0
Честно - я не знаю, как решать такое уравнение, наверное только графически.
Вольфра Альфа показывает один корень x0 ~ 11,0377; y(x0) ~ 6,1942
Это точка минимума.
6) При x Є (0; x0) функция убывает
При x Є (x0; +oo) функция возрастает
7) Точек перегиба нет, функция везде вогнута (выпуклая вниз).
8) Наклонных и горизонтальных асимптот нет.
9) lim(x -> 0) y(x) = +oo
lim(x ->+oo) = +oo
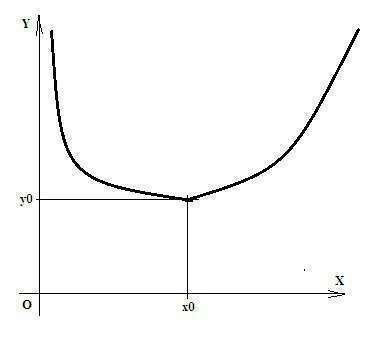
10) График примерный на рисунке