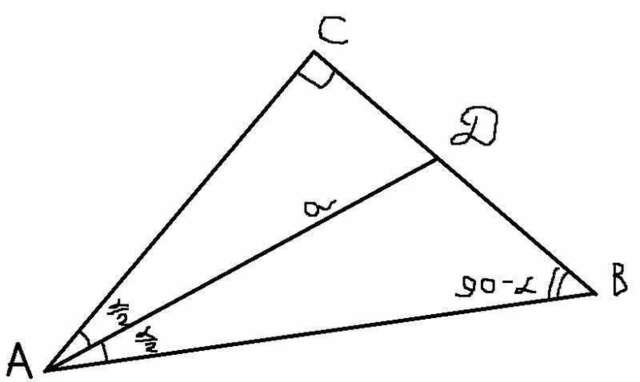
Для начала рассмотрим треугольник ACD. Вычислим катет АС. Здесь АD - гипотенуза, угол CAD равен  по определению биссектрисы AD.
по определению биссектрисы AD.


Катет CD равен


Теперь рассмотри исходный треугольник АВС. Найдем в нем другой катет СВ. Так как

то 


Заметим, что BD=CB-CD


Можно, конечно, упростить, но как-то неохота, да и будет ли проще?