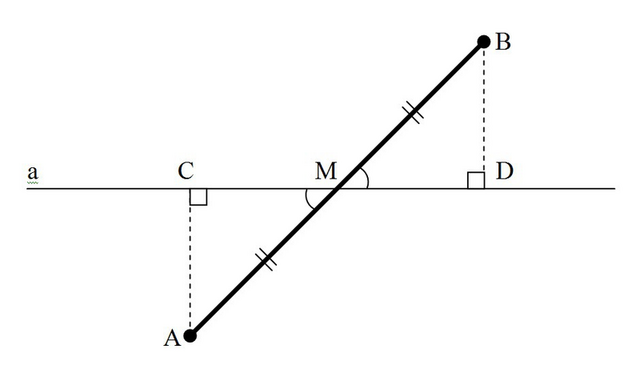
Чертеж прилагается ниже.
Дано: a ∩ [AB] = M
|AM| = |MB|
Доказать: |AC| = |BD|
Доказательство: При пересечении отрезком [AB] прямой а образуются
вертикальные углы ∠CMA = ∠BMD.
Так как расстояние от точки до прямой определяется перпендикуляром из этой точки на прямую, то:
∠ACM = ∠BDM = 90°
В треугольниках ΔMCA и ΔMDB:
∠ACM = ∠BDM = 90°
∠CMA = ∠BMD,
следовательно, ∠CAM = ∠MBD по теореме о сумме внутренних углов треугольника.
А, значит, ΔMCA = ΔMDB по стороне и двум прилежащим углам.
Так как в равных треугольниках соответственные стороны равны, то:
|AC| = |BD|, ч.т.д.