Найдите площадь круга вписанного в прямоугольную трапецию, основая которой равны 4 см и...

Question

Дано ответов: 2

Правильный ответ

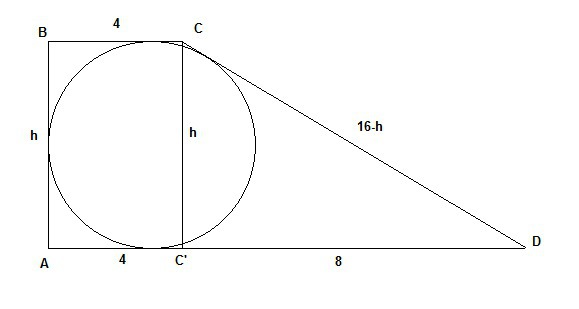
Так как в трапецию можно вписать окружность, то сумма ее оснований равна сумме боковых сторон. Одна из сторон является высотой трапеции, так как трапеция прямоугольная. Обозначим ее h. Тогда раз сумма оснований равна 16 см, то вторая боковая сторона равна 16см-h. Из C можно провести перпендикуляр СС' на основание трапеции AD. AC' = 4 см, следовательно, C'D=12 см - 4 см = 8 см.
Теперь рассмотрим прямоугольный треугольник CC'D. Для него выполняется соотношение CC'²+C'D²=CD².
Подставим обозначенные ранее величины.
h²+(8 см)²=(16 см - h)²
h² - 32 см * h + 256 см² =h² + 64 см²
32 см * h = 256 см² - 64 см²
h = 8 см - 2 см = 6 см
Очевидно, что высота трапеции - это диаметр вписанной окружности. Поэтому радиус окружности равен r = h/2 = 3 см.
S круга = πr² = 9π см².

iknowthatyoufeelbro_zn (16.7k баллов) 29 Апр, 18

Dimanolog107_zn · Answer 1 · 2018-04-29T13:43:26+0000

Если в прямоугольную трапецию вписана окружность, площадь трапеции равна произведению ее оснований.
Следовательно Sтрап=BC*AB=4*12=48см.кв.
Площадь трапеции равна произведению полусуммы ее оснований на высоту: Sтрап=(BC*AB)/2*AB
( $\frac{BC*AB}{2}*AB$ = 48;
подставим значения оснований
$\frac{4*12}{2}*AB$ =48;
24*AB=48;
AB=2;
Высота прямоугольной трапеции равна ее меньшей боковой стороне и равна диаметру вписанной окружности.
$S = \pi r^{2}$
$r= \frac{AB}{2}=1$
$S= \pi * 1^{2} = 3,14$

Dimanolog107_zn (23 баллов) 29 Апр, 18