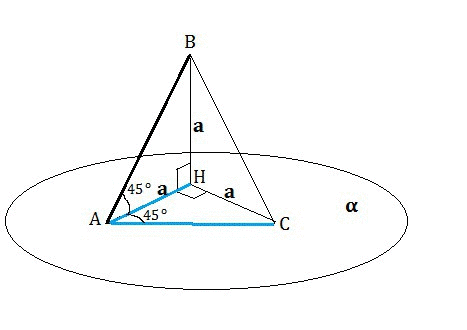
Опустим из В перпендикуляр ВН на плоскость α.
Пусть ВН=а
Δ АВН прямоугольный.
Сумма острых углов прямоугольного треугольника равна 90°⇒
∠АВН =90°-45°=45°.
Два равных угла - свойство равнобедренного треугольника. ⇒ АН=ВН=а
Проведем отрезок НС⊥АН до пересечения с прямой АС.
Δ АНС прямоугольный, а т.к. ∠НАС=45°, то ∠НСА=45°⇒
Δ ВНС - равнобедренный.
Соединим В и С
В прямоугольных треугольниках АВН, СВН, АСН - катеты равны а.
Следовательно, эти треугольники равны, из чего следует равенство их гипотенуз
АВ=ВС=АС.
Δ АВС - равносторонний, все углы равностороннего треугольника равны 60°⇒∠ВАС=60°, что и требовалось доказать.