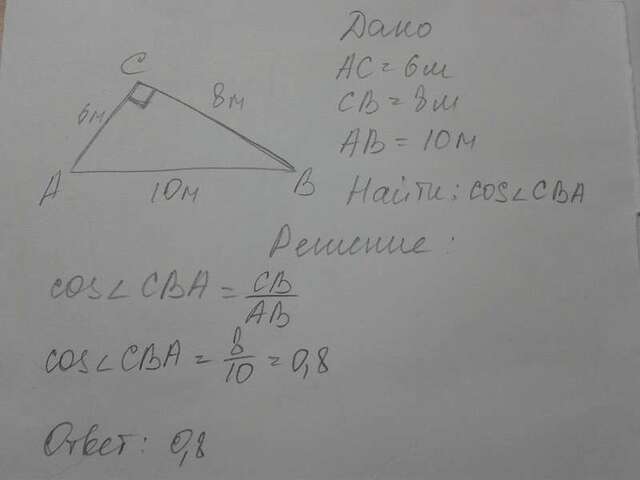1)Высота образует два прямоугольных треугольника, рассмотрим тот, в котором гипотеназой является боковая сторона, которая равна 13 см, в треугольнике незвестна только высота; по теореме Пифагора находим высоту - она равна 12 см
Площадь равна 12*13/2=78
2)
.Пускай трапеция называется АВСД
2.првести высоту СМ в трапеции с тупого угла к большей основе
3. расмотреть треугольниу СМД, СМ=16√2*√2/2=16см
√2/2(синус 45)
4. МД=16(равнобедренный треугольник СМД)
5. треугольник АВС
ВС=√400-256=√144=12(теорема пифагора)
6. площадь: (ВС+АД)/2*СМ=(12+12+16)/2*16=320
периметр:12+12+16+16√2+16=56+16√2
3)Попробуйте так:
АВСD - параллелограмм,
АВ = 24, АD = 25, ВD - диагональ, ВD= 7
Рассмотрите треугольник АВD.
В нем известны все стороны, они равны 25, 24 и 7.
Поскольку 25^2 = 24^2 + 7^2, то есть квадрат стороны треугольника равен сумме квадратов двух других сторон, то этот треугольник прямоугольный.
Значит, угол АВD = 90 градусов.
Расстояние между прямыми, содержащими меньшие стороны параллелограмма - это длина перпендикуляра, опущенного с одной стороны на другую.
Таким перпендикуляром будет диагональ ВD. А она по условию равна 7. Значит, расстояние между прямыми, содержащими меньшие стороны параллелограмма равно 7
4)По определению ромба: Ромб – "четырёхугольник, у которого все стороны равны между собой" можно сделать вывод, что для доказательства необходимо определить, равны-ли стороны: BM, MD, DN, NB.
Рассмотрим треугольники ABM и NBC - они равны, т.к. сказано, что отрезки AM и CN - равные, а стороны AB и BC - стороны квадрата, а так же диагональ в квадрате делит углы поровну (т.е. по 45°) => BM=NB.
То же самое и со сторонами MD и ND: треугольники AMD и NDC -равные по двум сторонам и углу => MD=ND.
отрезки AM и CN - общие для треугольников ABM, NBC и AMD, DNC соответственно. А AB=BC=AD=CD(т.к. стороны квадрата) => треугольники ABM, NBC, AMD, DNC - равные => MD=NB=MD=ND =>BNDM - ромб.
5)Нет, не может, так как сумма 20/2 и 22/2 = 21 (это сумма 2-х сторон треугольника, а она всегда больше третьей стороны)
6)
Рассмотрим треугольник АВМ
1) угол ВАМ=углу МАК, так как АМ-биссектриса угла А
2) угол ВАМ= углу ВМА-внутренние накрест лежащие при ВС параллельно АД, АМ-секущая
следовательно треугольник АВМ- равнобедренный, следовательно ВМ=АВ=6 см
АВ=СД=6см
Рассмотрим треугольник СКД
1) угол МСК=углу ДСК, так как СК-биссектриса угла С
2) угол МСК=углу СКД- внутренние накрест лежащие при ВС параллельно АД, СК-секущая
следовательно СД=АК=6 см
АД=ВС=6+4=10см
периметр АВСД=2(10+6)=32 см
7)
8)
Дана прямоугольная трапеция ABCD
AC - диагональ
ACD - равносторонний тр.
AD=12 см
Найти:
MN - ср. линия - ?
Решение:
Так как ACD равносторонний (AC=CD=AC=12 см), то все его углы 60⁰.
След-но угол BAC = 90⁰-60⁰=30⁰ ⇒ угол ACB = 60⁰
Катет лежащий против угла в 30⁰ равен половине гипотенузы ⇒ BC=1/2*AC = 6 см
MN=1/2*(BC+AD) = 1/2*(6+12) = 1/2*18 = 9 см
Ответ. средняя линия равна 9 см
9)Соединим середины сторон всеми возможными способами. Ромб ABCD, в него вписан (как легко убедиться) прямоугольник MKLN, диагонали пересекаются в точке O. Получили 4 маленьких ромба: AMON, MBKO, OKCL, NOLD. В каждом из этих ромбов часть прямоугольника равна половине площади ромба. Отсюда площадь прямоугольника равна половине площади ромба, т.е. S/2.
Ответ: S/2
10)ты уже написал,это 2 задачка.
11)Пусть ABC - треугольник. М - середина АВ, N - середина ВС, К - середина АС.
Докажем, что треугольники AMK, BMN, NKC, MNK равны.
Так как M,N,K - середины, то
AM = MB, BN = NC, AK = KC.
Используем свойство среднее линии:
MN = 1/2 * AC = 1/2 * (AK + KC) = 1/2 * (AK + AK) = AK
Аналогично MK = NC, NK = AM.
Тогда в треугольниках AMK, BMN, NKC, MNK
AM = BM = NK = NK
AK = MN = KC = MN
MK = BN = NC = MK
12)Осей симметрии у ромба (если он не квадрат) всего две - это его диагонали. PM перпендикулярна AC (т.к. PM парралельно BD, а BD перпендикулярна AC по св-ву диагоналей ромба), как и KH (аналогично). PK параллельна AC, как и MH, а значит они обе перпендикулярны BD => MPKH - прямоугольник
Т.к E и Т лежат на АС, то и EPKH тоже прямоугольник