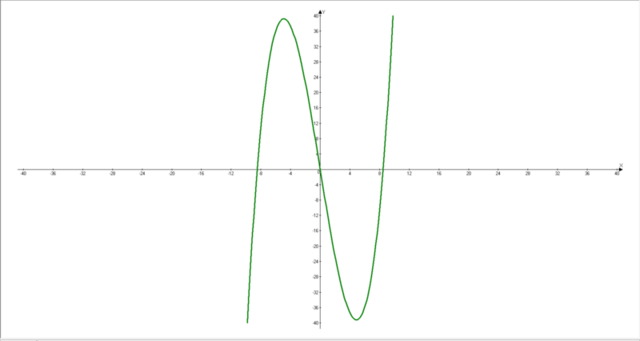
1)D(y)=R;E(y)=R
2)F(-x)=-1/6*x^3+12x функция нечетная
3)Точки пересечений:
Ох: x(1/6*x^2-12)=0
x=0 ; x^2=72
x=+-\sqrt72
Oy: y=0
4)f`(x)=x^2/2-12=0
x=+-\sqrt(24)
ф-я возрастает от (-беск.-\sqrt(24));(sqrt(24);+беск.)
ф-я убывает от (-\sqrt(24);sqrt(24)
x(max)=-\sqrt(24) x(min)=\sqrt24
5)Точки перегиба:
f``(x)=(1/6*x^3-12*x)=x=0
Т.пер:х=0(Вроде бы так)
У нас в школе обычно так описывали функцию.Извиняюсь за сколь "корявое описание" просто в редакторе писать долго.а сам график во вложении.Да и еще недочет в том что из под корней можно вытащить числа...