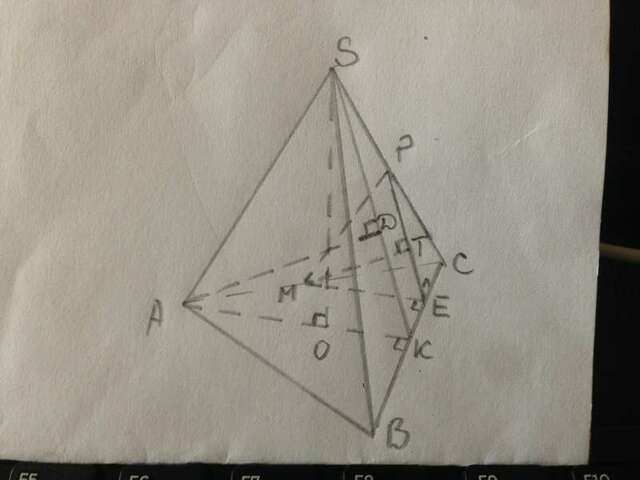
В основании АВС проведём высоту АК. АК=а√3/2=ВС√3/2=4√3.
МЕ - перпендикуляр к ВС. МЕ - средняя линия тр-ка АСК, значит МЕ=АК/2=2√3.
РЕ - перпендикуляр к ВС. РЕ - средняя линия тр-ка SКС. SP=CP ⇒ РМ - средняя линия тр-ка SAC, значит треугольники SAK и РМЕ подобны с коэффициентом подобия k=АК/МЕ=2
SK=√(SB²-СK²)=√(15²-4²)=√209.
SO - высота пирамиды. Точка О - центр описанной окружности около правильного тр-ка АВС, значит R=АО=АК·2/3=8√3/3.
В тр-ке SAO SO=√(SA²-AO²)=√(15²-(8√3/3)²)=√(611/3).
Площадь тр-ка SAK: S=AK·SO/2=4√3·√611/(2√3)=2√611.
АД⊥SK.
Площадь того же тр-ка: S=АД·SK/2 ⇒ АД=2S/SK=4√(611/209).
В тр-ке МРЕ МТ⊥РЕ.
АК║МЕ, SA║MP, SK║PE, значит плоскости тр-ков SAE и МРЕ параллельны. АД⊥SBC ⇒ МT⊥SBC.
Из подобия треугольников SAK и МРЕ МТ=АД/k=2√(611/209) - это ответ.