1. Выразим у из первого уравнения и подставим во второе
{у=|x-3|
{x·|x-3|=4
Решаем второе уравнение. Применяем определение модуля.
Если х-3≥0, то |x-3|=x-3
x·(x-3)=4
x²-3x-4=0
D=(-3)²-4·(-4)=9+16=25=5²
x=(3-5)/2=-1 или х=(3+5)/4
х=-1 не удовлетворяет условию х-3≥0
поэтому не является корнем уравнения
при х=4
у=|х-3|=|4-3|=1
Если х-3<0, то |x-3|=-x+3<br>x·(-x+3)=4
x²-3x+4=0
D=(-3)²-4·4=9-16<0<br>уравнение не имеет корней.
Решение системы
{х=4
{у=1
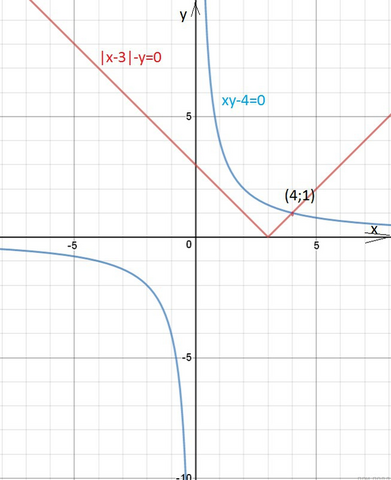
Cм. графическое решение в приложении
О т в е т. А) один
2.
{x-y=16
{√x+√y=8
По формуле разности квадратов
х-у=(√х-√у)·(√х+√у)
{(√х-√у)·(√х+√у)=16
{√x+√y=8
{(√х-√у)·8=16
{√x+√y=8
{√х-√у=2
{√x+√y=8
2√х=10 ⇒√х=5⇒ х=25
у=х-16=25-16=9
х·у=25·9=225
О т в е т. Д)225