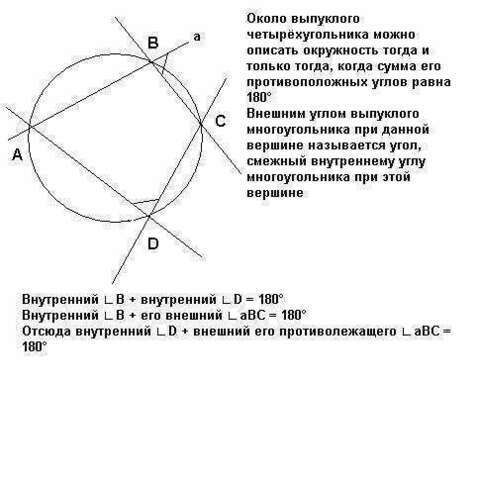
Цитата: "Около выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна 180°
Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине".
Пусть будет четырехугольник АВСD вписан в окружность. Тогда сумма любых его противолежащих внутренних углов равна 180°. Но сумма любого внутреннего угла и соответствующего ему внешнего тоже равна 180° ( как смежного).
Значит этот смежный внутреннему угол равен противолежащему внутреннему.
Что и тр. док.