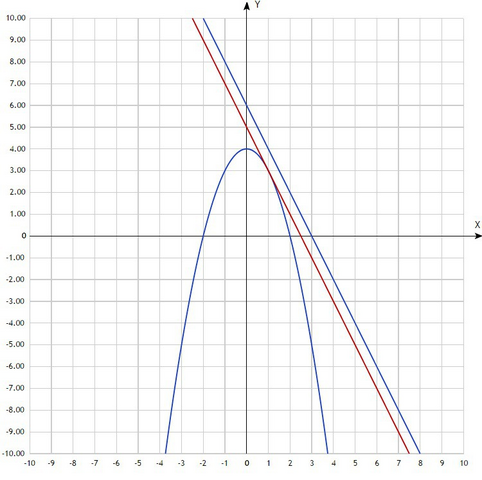
Y=f(x₀)+f'(x₀(x-x₀) - уравнение касательной.
По условию касательная параллельна прямой y=-2x+6, значит коэффициент наклона прямой равен -2, а коэффициент наклона касательной есть значение производной в точке касания. Найдём точки, в которых производная функции y=-x²+4 равна -2. Сначала найдём производную
y'=(-x²+4)'=-2x
Приравняем производную к числу -2
-2x=-2
x₀=1
Найдём уравнение касательной к графику функции y=-x²+4 в точке x₀=1.
Найдем значение функции в точке x₀=1.
f(1)=-1²+4=3
f'(1)=-2 (по условию)
Подставим эти значения в уравнение касательной
y=3+(-2)(x-1)=3-2x+2=-2x+5