1.** рисунке 280 точка О центр окружности угод ABO=40 градусам. Найдите угол BOC 2.К...

Question

1.На рисунке 280 точка О центр окружности угод ABO=40 градусам. Найдите угол BOC
2.К окружности с центром О провели касательную CD(D точка касания). Найдите радиус окружности, если CO=16 см и угол COD=60градусов

Answer 1

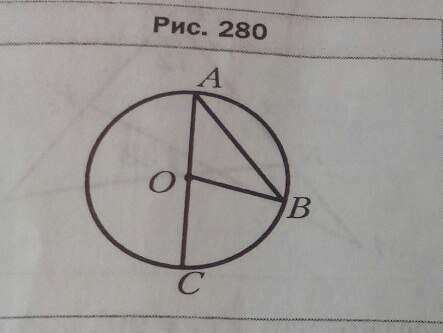
1. ОА = ОВ как радиусы, ⇒ ΔАОВ равнобедренный.
∠ВАО = ∠АВО = 40°.
∠ВОС - внешний угол треугольника АВО. Внешний угол треугольника равен сумме двух внутренних, не смежных с ним:
∠ВОС =  ∠ВАО + ∠АВО = 40° + 40° = 80°

2. Радиус, проведенный в точку касания, перпендикулярен касательной:
∠ODC = 90°.
Из ∠ODC:
 OD = OC · cos 60° = 16 · 0,5 = 8 см

---