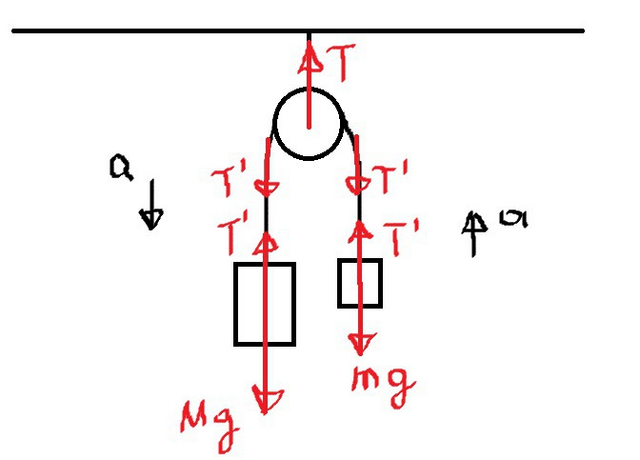
1) построим чертеж с указанием всех сил, действующих на грузы и блок (в чертеже использован 3 закон Ньютона)
2) допуская, что блок невесомый, запишем уравнения динамики:
T - T' - T' = 0,
T - mg = ma,
Mg - T = Ma.
складывая второе уравнение системы с третьим, получим:
g (M - m) = a (m + M),
a = g (M - m) / (m + M).
исходя из уравнения динамики для блока мы можем утверждать, что:
T = 2 T'.
по условию T = Mg.
из первого уравнения системы получим, что:
T' = mg + ma.
значение T' представим как (Mg)/2, а ускорение как g (M - m) / (m + M). тогда получим:
M = 2m (1 + (M-m)/(m+M)),
M = 2m * ((2M)/(m+M)),
4 m M = M m + M².
введем параметр x = M/m и разделим обе части получившегося уравнения на m²:
4 x = x + x²,
x² - 3x = 0,
x (x - 3) = 0,
x = 3
x = 0 - не подходит