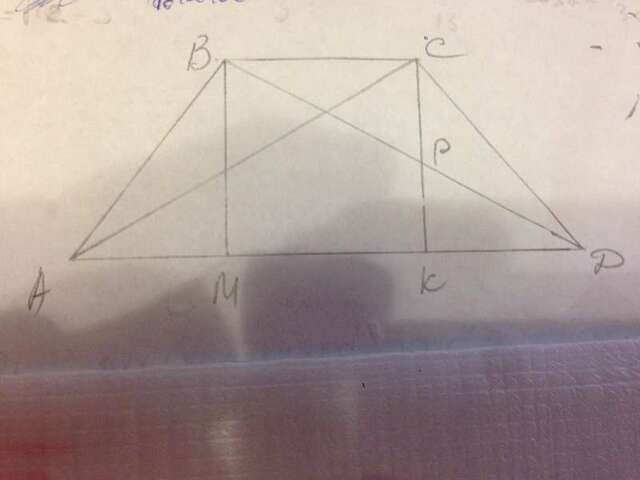
АВСД - трапеция, АД=25 см, ВС=7 см. ∠АВД=АВД=90°.
ВМ и СК - высоты на сторону АД.
АМ=(АД-ВС)/2=(25-7)/2=9 см. АМ=КД.
МД=АД-АМ=25-9=16 см.
В тр-ке АВД ВМ=√(АМ·МД)=√(9·16)=12 см.
Диагональ ВД пересекает высоту СК в точке Р.
Треугольники ВДМ и КРД подобны по трём углам.
ВМ/РК=МД/КД ⇒ РК=ВМ·КД/МД,
РК=12·9/16=6.75 см.
СР=12-6.75=5.25 см.
Ответ: высота делится на отрезки 6.75 и 5.25 см.