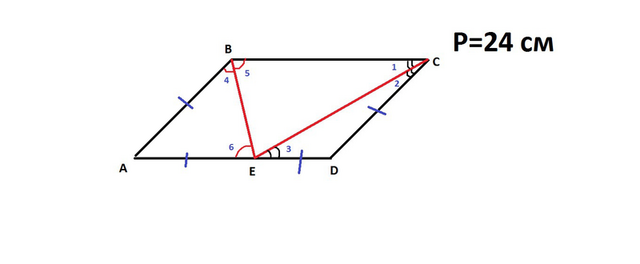
Р=(a+b)*2 -периметр, где а и b -стороны параллелограмма АВСD
биссектриса делит угол пополам, значит ∠1=∠2 и ∠4=∠5
∠1=∠3 - так как они накрест лежащие при параллельных прямых AD и BC и секущей СЕ, следовательно ∠2=∠3, значит Δ СЕD -равнобедренный и DE=CD
∠5=∠6 - так как они накрест лежащие при параллельных прямых AD и BC и секущей ВЕ, следовательно ∠4=∠6 значит Δ ВАЕ -равнобедренный и АВ=АЕ
АB=CD - по свойству параллелограмма, отсюда следует, что АВ=AE=CD=DE
Путь АВ=AE=CD=DE = х
AD=AE+ED=x+x=2x, тогда
P=(x+2x)*2
3x*2=24
6x=24
x=4
2x=2*4=8
отв: 8 см