Есть два решения(т.к не сказано, какой именно угол 140*) .
1 способ
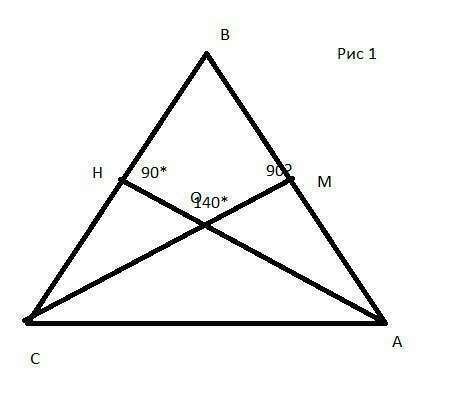
Дан треугольник АВС (АВ=ВС), АН,СМ - высоты, ∠НОМ
=140*(или ∠СОМ т.к они вертикальные, то они равны)
Рассмотрим четырехугольник НОМВ
∠ОНВ=∠ОМВ=90*(свойство высоты) ,∠НОМ=140*
Сумма углов в четырехугольнике равна 360*
∠НВМ =360-90-90-140=40
Вернемся к треугольнику АВС(сумма углов 180*,∠С=∠А=х)
2х=180-40
2х=140
х=70*
Второй вариант.
∠МОА =140*(или ∠ВОН)
∠МОА,∠НОМ - смежные (их сумма 180*)
∠НОМ =180*-140*
∠НОМ =40*
Снова рассмотрим четырехугольник НОМВ
∠НВМ =360-90-90-40=140*
2х=180-140
2х=40
х=20*