Дробь равна 0 тогда и только тогда когда числитель равен 0, а знаменатель отличен от нуля.
sinx+(1/2)=0;
cos(x+π/3)≠0
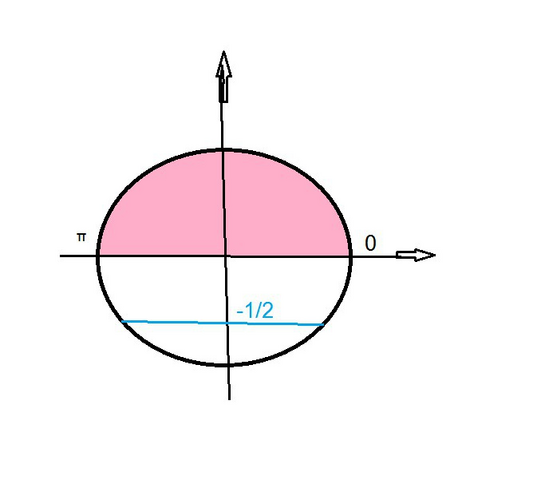
sinx=-1/2
Корни уравнения в третьей и четвертой четвертях, там синус принимает отрицательные значения и ни один из корней не находится на отрезке [0;π].
Cм рисунок.